Reliable method of determining stable threshold channel shape using experimental and gene expression programming techniques

Abstract

The geometric dimensions and bank profile shape of channels with boundaries containing particles on the verge of motion (threshold channels) are significant factors in channel design. In this study, extensive experimental work was done at different flow velocities to propose a reliable method capable of estimating stable channel bank profile. The proposed method is based on gene expression programming (GEP). Laboratorial datasets obtained from Mikhailova et al. (Hydro Tech Constr 14:714–722, 1980), Ikeda (J Hydraul Div ASCE 107:389–406 1981), Diplas (J Hydraul Eng ASCE 116:707–728, 1990) and Hassanzadeh et al. (J Civil Environ Eng 43(4):59–68, 2014) were used to train, test, validate and examine the GEP model in various geometric and hydraulic conditions. The obtained results demonstrate that the proposed model can estimate bank profile characteristics with great accuracy (determination coefficient of 0.973 and mean absolute relative error of 0.147). Moreover, for practical calculations of channel dimensions, the model provides a specific mathematical relationship to solve problems with different discharge rates (Q) and particles with various median grain sizes (D₅₀). The proposed model’s performance is compared with 8 relationships suggested previously by researchers (based on empirical and theoretical analyses) and a relationship obtained using a nonlinear regression model with different experimental data. The polynomial VDM and two exponential functions, i.e. IKM and DIM, are introduced as the superior existing models. According to the present study results, the proposed GEP model can predict the bank profile shape trend well and similar to the experimental datasets. Sensitivity analysis was also applied to assess the impact of each input variable (x, Q and D₅₀) on the presented relationship. According to the current study, the GEP model provides a suitable equation for predicting the bank profile shape of stable channels.

1 Introduction

River science engineering requires determining the threshold conditions in natural rivers and irrigation channels for design purposes. The threshold or static equilibrium status of a channel is the final stage of channel widening [48], when the channel’s cross-sectional area reaches the smallest value. The geometric profile of a threshold channel’s cross section is determined according to the properties of flow and materials on the channel bed. If the side slope is defined, it is possible to calculate the geometric shape of a channel with a specified central depth. Yu and Knight [57] defined two common methods of determining the geometric shape of a threshold channel. One of the methods is established on the channel widening procedure, whereby channel widening is simulated using numerical modelling of the bed shape change. This widening process occurs when the rate of sediment transport at any point on the wall is gradually removed and a threshold channel forms accordingly. The second method considers the equilibrium of the effective shear force on particles at any point on the bed, the shear stress value at the incipient motion of sediment and the flow discharge to calculate the threshold condition of materials on the channel’s side slope. Glover and Florey [26] were the first who studied the notion of a stable channel profile. Stebbings [52], Mikhailova et al. [40] and Macky [37] subsequently carried out extensive experimental investigations on the bank profile shapes of stable channels. Parker [47] employed an evolutionary method to determine the distribution of mobile bed shear stress in channels with certain flow velocities. Ikeda et al. [31] presented a model for predicting the depth and width of rivers with gravel beds. They affirmed that the main factor affecting channels in stable state is lateral diffusion due to fluid turbulence. Moreover, the first effective parameters in determining stable channel geometry were introduced as the flow velocity, free-surface longitudinal slope and average size of particles on the bed. Cao and Knight [4] proposed a geometric model including flow continuity, frictional resistance, sediment transport, and bank profile-based entropy profile equations. Cao and Knight [4] stated that the bank profile shape is a polynomial curve. Mironenko et al. [41] deduced that the shape of a channel’s transverse profile is a parabolic curve, while Diplas [6] and Pizzuto [49] suggested an exponential function shape. Diplas and Vigilar [7] used a numerical model and solved the momentum, fluid and energy balance equations for sediment particles in impending motion. They also presented some relationships for predicting channel stability. Their results suggested a polynomial of degree five for the predicted bank profile, which is quite different from conventional threshold bank shapes, such as cosine, parabolic and exponential. Vigilar and Diplas [55] suggested an exponential equation for bank profile calculation. The optimum existing channel profile shape is polynomial. Vigilar and Diplas [56] subsequently suggested the third-degree polynomial. Babaeyan-Koopaei and Valentine [3] evaluated stable alluvial channel profile geometry experimentally and compared the results with previously published equations. Apparently, the polynomial equation recommended by Diplas and Vigilar [7] leads to better estimation with the normal-depth method. The researchers suggested two hyperbolic functions for predicting channel cross-sectional shape. Dey [5] presented a modified model to calculate the cross-sectional dimensions of a threshold channel. Macky [38] proposed two models, namely a conventional and a diffusive model to describe the widening process in stable channels.

In recent decades, various soft computing methods have been applied for modelling complex phenomena. Many researchers have used soft computing to model a diversity of engineering cases, such as simulating open channel bends [19,20,21,22,23,24], predicting the discharge in flow diversion structures, such as weirs and side orifices [8, 34], and scouring [45]. Based on the authors’ knowledge, the only method ever used for predicting the bank profile shape of stable channels involves artificial neural networks (ANN). Khadangi et al. [32] employed ANN to model the geometry of alluvial channels and compared the results with semi-empirical equations. Madvar et al. [39] used a multi-layer perceptron neural network (MLPNN) to estimate stable channel dimensions. Taher-Shamsi et al. [53] employed ANN modelling to predict stable channel width and compared the results with regression equations. Shamsi et al. emphasized the high ANN model accuracy in predicting stable channel dimensions. One of the major setbacks of ANN models is the absence of a specific relationship for use in practical applications. Gholami et al. [25] evaluated GMDH performance in designing stable channel width, depth and slope for instance. Their results validated the high efficiency of the proposed GMDH model. However, they did not discuss bank profile shape in stable state nor assessed equations governing the stable bank profile. Shaghaghi et al. [51] compared a GMDH model with a particle swarm optimization evolutionary algorithm in estimating stable channel width. They declared that the generalized structure of the GMDH type (GS-GMDH) based on GA is more efficient that GMDH-PSO in making predictions.

As a subset of genetic algorithms, gene expression programming (GEP) is very popular with researchers (e.g. [2, 9, 17, 18, 27, 42, 46, 58]) because GEP facilitates the precise prediction of hydraulic phenomena and consumes less calculation time. In general, the major problem with some soft computing models (such as ANN and ANFIS) is the presence of complex rules that prevent these models from providing relationships for predicting variables regarding different inputs for use in various applications. The unique properties of the GEP model and its multi-genic nature facilitate complex program improvement [15]. One of the noteworthy advantages of GEP over ANN is that GEP models provide an efficient and transparent modelling solution [28]. Moreover, GEP models have the powerful ability to generate equations for predicting variables [15, 43]. In a GEP model, the most important prediction set is selected and it does not require setting many parameters. These advantages render GEP a simple model for common uses [10, 50].

The main aim of the current study is to present a reliable GEP model for predicting the bank profile characteristics of stable channels. Therefore, a vast experimental study was carried out using discharge rates of 1.157, 2.18, 2.57 and 6 l/s to predict stable channel shape. In addition, extensive experimental data obtained by other researchers in various hydraulic and geometric conditions in different countries were applied to create the proposed models. A remarkable advantage of GEP is the possibility to extract a simple mathematical relationship for problem solving. GEP modelling also facilitates determining an appropriate channel profile geometric shape by using different discharge rates and median grain sizes. The proposed GEP model results are compared with 8 theoretical and experimental relationships, and the superior model is introduced. Sensitivity analysis of the different input parameters for predicting stable channel shape is carried out as well.

2 Materials and methods

This section presents the various models used to predict stable channel shape, the experiments performed, the optimum GEP model and the model assessment criteria.

2.1 Overview of existing models

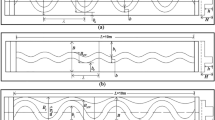
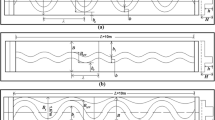
The shape of a channel in stable state is significant to bank profile geometric shape formation. Figure 1 illustrates two bank profile characteristics. In this figure, x and y (m) are the transverse and vertical distances from the bed centre, respectively, h is the flow depth at the centre line and T is the water surface width. The bank profile characteristics are dimensionless (y^* = y/h, x^* = x/h and T^* = T/h) and shown in Fig. 1.

Fig. 1

Sketch of geometric characteristics

Vigilar and Diplas [55] presented the following relationships to determine h and T^*:

$$h = \frac{{(S_{\text{s}} - 1)d_{50} }}{{\delta_{\text{cr}}^{ * } }}\tau_{\text{c}}^{ * }$$

(1)

$$T^{ * } = \frac{T}{h} = - 16.1814\mu^{3} + 44.3206\mu^{2} - 43.5548\mu + 21.1496$$

(2)

where h = the depth at the bed centre in stable condition, T^* = dimensionless water surface width, ρ_s = sediment density, ρ = water density, d₅₀ = mean sediment size (m), S_s = ρ_s/ρ = relative density, $\tau_{\text{c}}^{ * } = {{\tau_{\text{c}} } \mathord{\left/ {\vphantom {{\tau_{\text{c}} } {\rho gd_{50} R_{\text{s}} }}} \right. \kern-0pt} {\rho gd_{50} R_{\text{s}} }}$ is the dimensionless critical shear stress, $\tau_{\text{c}}$ = critical shear stress, g = gravitational acceleration, R_s = (ρ_s − ρ)/ρ is the submerged specific gravity of sediment, and $\delta_{\text{cr}}^{ * }$ = the critical bed stress depth that is obtained as follows:

$$\delta_{\text{cr}}^{ * } = - 0.0223\mu^{3} + .01481\mu^{2} - 0.31403\mu + 1.031$$

(3)

where μ = tan(θ) is the submerged coefficient of the static friction of sediment particles and θ is the angle of repose of sediment. Yu and Knight [57] presented an empirical equation for μ as follows:

$$\mu = \tan \left[ {\begin{array}{l} {0.302\left( {\log 100d_{50} } \right)^{5} + 0.126\left( {\log 100d_{50} } \right)^{4} } \\ { - 1.811\left( {\log 100d_{50} } \right)^{3} - 0.57\left( {\log 100d_{50} } \right)^{2} + 5.952\left( {\log 100d_{50} } \right) + 37.52} \\ \end{array} } \right]$$

(4)

τ ^*_c has a dimensionless value that may be obtained from Van-Rijn’s [54] equations, where $D^{*} = d_{50} \left[ {\frac{{\left( {S_{\text{s}} - 1} \right)g}}{{\nu^{2} }}} \right]^{{{1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-0pt} 3}}}$ is the dimensionless particle size and ν is the kinematic viscosity of water. Table 1 lists the relationships examined in this study and proposed by Glover and Florey [26], Ikeda [30], Pizzuto [49], Diplas [6], Babaeyan-Koopaei and Valentine [3], Cao and Knight [4], Vigilar and Diplas [56] and Dey [5]. These relationships were achieved from numerical, experimental or field models based on analytical, mathematical, theoretical or regression relationships. The abovementioned relationships are expressed in the present study as follows: GFM (Glover and Florey’s Model), IKM (Ikeda’s Model), PIM (Pizzuto’s Model), DIM (Diplas’ Model), VDM (Vigilar and Diplas’ Model), CKM (Cao and Knight’s Model), BVM (Babaeyan-Koopaei and Valentine’s Model) and DEM (Dey’s Model).

Table 1 Models investigated in this study

2.2 Experimental model

In the present study, ten experimental datasets were used for model assessment. The laboratorial data obtained from Ikeda [30], Mikhailova et al. [40] (two sets), Diplas [6] and Hassanzadeh et al. [29] (two sets), and four datasets from the current laboratorial work were used to train, test and calibrate the models for stable channel bank profile estimation. The data applied in the models consist of several lateral points on the lateral profile of a channel’s mobile bed. All experiments were done in laboratory flumes. The sediment was coarse and the flow shallow to avoid ripple formation. The Froude number was larger than the dune formation range [6].

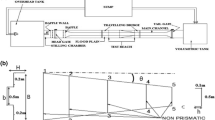
In addition, four sets of experiments were carried out to measure the bank profile parameters. The flume employed was 20 m long, 1.22 m wide and 0.6 m deep. The flume bed was filled with uniform sand with d₅₀ of 0.53 mm and standard deviation (σ) of 1.23. For the experiments, two trapezoidal and triangular-shaped cross sections were selected. Flow passed through the channel at four velocities, each of which remained constant until stable channel state was attained. A magnetic flow metre was used to measure flow velocity. For each discharge rate (flow velocity), a 0.23% slope was fixed using a wooden former fixed on a carriage. Each test set continued until stable channel state was achieved at the plane and cross sections. All experiments were carried out for 10–12 h each until stable channel state was achieved. Finally, the geometry of the cross sections and bank profile was recorded. Two free water surface and channel bed levels were measured using a point gage at transverse distances of 8, 9 and 11 m from the channel entrance [33]. Table 2 summarizes the characteristics of the experimental sets conducted by Ikeda [30], Mikhailova et al. [40], Diplas [6] and Hassanzadeh et al. [29] as well as the current laboratorial work. The laboratorial flume used in the current study is shown in Fig. 2.

Table 2 Experimental characteristic summary of the data used in the present study

Fig. 2

Laboratorial model

2.3 Gene expression programming (GEP) model

GEP is a linear-based genetic programming method presented by Ferreira [11] and developed from two evolutionary algorithms, namely the genetic algorithm (GA) and genetic programming (GP). GA presents the estimated results only in numerical form but GP solves the GA problem using a specified mathematical relationship and a computer program with a tree structure [36]. Ferreira [11] exploited the benefits of using both GA and GP simultaneously to overcome the shortcomings of the two individual methods. Because GEP uses different genetic operators in the chromosomes, it leads to genetic diversity. This method is also considered multigenetic, which leads to more various complex programs [11,12,13]. To obtain a solution for a specific problem, GEP employs fixed-length character sequences and presents the solution as parse trees, or expression trees (ETs) [1] of different shapes and sizes [44]. The main components of the GEP algorithms include the control, fitness function, function set, terminal set and terminal condition parameters [44]. Each gene in GEP includes a fixed-length set of symbols that can be any components of the terminal set {Z, L, M, N, − 1} or function set {+, −, ×, /, √, tan, cos} [1]. For instance, for a chromosome with two genes consisting of four functions {√, ×, /, +} and three terminals (a, b, c), the related algebraic expression is $(a/b) + (\sqrt {a \times b} )$. The GEP modelling process is initialized with the random generation of a primary chromosome population. Each individual chromosome in the initial population is evaluated using the fitness function defined for the problem. Fitness functions may include mean square error (MSE), root mean square error (RMSE), root relative square error (RRSE) and relative square error (RSE) [2, 11, 35]. However, owing to the widespread use and good RRSE results in various studies [35], this fitness function is used in the current study. Chromosomes deemed to have superior fitness function values are selected for use in the next generation. Subsequently, the selected chromosomes are adapted using genetic operators. Several genetic operators used for chromosome modification are: mutation, inversion, three transportation operators and three recombination operators, which are defined as follows:

2.3.1 Mutation

Mutation can happen anywhere in the chromosome. The existing function at the chromosome head can be switched with a function or terminal, but at the tail, a terminal must be exchanged only with another terminal. Therefore, mutation helps maintain structurally organized chromosomes and structurally correct programs when using the new individuals generated by this operator. There are no imperatives regarding the number or type of mutations in a certain chromosome. Mutation is done at point 0 on gene 1, point 3 on gene 2 and point 1 on gene 3 (Fig. 3).

Fig. 3

GEP model genetic operators

2.3.2 Inversion

This genetic operator is limited to the gene head and inverts a selected sequence in the gene head. To modify the gene, the terminal and initial points of the head portion are inverted through the random selection of chromosomes. With the inversion operator, each chromosome is changed only once. In Fig. 3, inversion is conducted at gene 2, whereby sequence adjkb is the inverse of sequence bkjda.

2.3.3 IS transposition

The insertion sequence (IS) transposition elements are selected randomly throughout the chromosomes. These elements are short genomic fragments with a terminal or function in the first position. IS transposition randomly selects a chromosome, a gene to be reclaimed, the start of an element, the target site and the transposon length. Considering a chromosome with two genes (Fig. 3), sequence bba was selected in the second gene for the IS component. Bond 6 in gene 1 was chosen to be cut and sequence bba was copied in the insertion place. With this operator, the sequence upstream of the insertion position remains unaltered, though the sequence downstream of the replicated IS component is eliminated at the head end, so in the examples, a*b is eliminated. It should be noted that insertion does not change the chromosome structural organization and the newly generated individuals are suitable programs. Moreover, the transposition results in extreme expression tree changes, which means a great adjustment occurs upstream of the insertion area.

2.3.4 RIS transposition

The difference between IS and root insertion sequence (RIS) is at the starting point. The starting point for IS can be a function or terminal, whereas for RIS it is always a function. Therefore, the RIS components are selected between head sequences. After randomly selecting a point in the head, the gene is checked downstream to find a function. If no function is found, the RIS operator is ineffective. The results of RIS transportation copying in the gene root are presented in Fig. 3. Here, sequence +bb in gene 2 of a chromosome with two genes is considered a component of RIS transposition.

2.3.5 Gene transposition

With this operator, a complete gene operates as a transposon. The gene transposition operator transposes itself to the beginning of the chromosome and deletes the gene at the place of origin, unlike IS and RIS transposition. Therefore, the chromosome length is maintained. Random selection is considered to select the chromosome that undergoes gene transposition and one of its genes except the first one is selected for transposition. An example of gene transposition is presented in Fig. 3.

2.3.6 One-point recombination

In one-point recombination, the crossover point is selected randomly and the parent chromosomes are coupled at similar points. The gene’s contribution following the crossover point is replaced among two chromosomes, generating two daughter chromosomes (Fig. 3).

2.3.7 Two-point recombination

In two-point recombination, two crossover points are selected randomly and two parent chromosomes are coupled. Two new chromosomes are produced by replacing the material among two crossover points. In this operation, the first gene of both parents is cut downstream of the termination point. Gene 2 related to chromosome 1 is split downstream of the termination point. Moreover, the second gene related to chromosome 2 is cleaved upstream of the termination point (Fig. 3). Two-point recombination is more powerful than one-point recombination and is fruitful for the evolution of more complex problems, chiefly when using multi genetic chromosomes with multiple genes.

2.3.8 Gene recombination

In this operation, there are gene replacements among two parent chromosomes, creating daughter chromosomes that include genes from the two parents. The displaced genes are selected casually and situated in identical locations as the parent chromosomes. The newly generated individuals consist of genes from the two previous parents. In this operation, similar genes replace each other and most times, the replaced genes differ from the previous ones and new materials are created. In gene recombination, new genes have different arrangements from existing genes, and this operator is not capable of producing new genes.

Chromosomes thus reproduce through this process, which continues until a stopping criterion is fulfilled. Figure 4 displays the proposed method flowchart.

Fig. 4

GEP flowchart

2.4 Deriving stable channel bank profile characteristics for GEP modelling

To generate the initial population, a chromosome with three different genes is used. According to Ferreira [11], the initial population number should be determined based on the 30–100 range, and in this study, the population number selected was 30. By considering other effective modelling parameters as fixed, the initial population was larger. However, even with a population increase no significant changes in modelling results were observed. The best value obtained for the preliminary population was 80. Then the fitness of every individual was estimated with the following equation:

$$f_{i} = {{1000} \mathord{\left/ {\vphantom {{1000} {(1 + E)}}} \right. \kern-0pt} {(1 + E)}}\quad E_{i} = P_{ij} - O_{j}$$

(5)

where O_ij and P_ij are the observed value and value obtained using the ith individual chromosome for fitness case j. The optimum result was achieved when the observed and predicted values were equal (E_ij = 0). Subsequently, the function and terminal set were selected. To select the function set, {+, −, ×, /} was used first. Trial and error was employed to improve modelling accuracy and additional functions were added separately. Function set {+, −, ×, /, x², x⁴, x⁵, $\sqrt[5]{x}$, Ln} was ultimately considered and the terminal set was as follows:

$$T = \left\{ {y, Q, x} \right\}$$

(6)

The head/tail length and number of genes were obtained by trial and error. Three genes were used in each chromosome and the head length was 7. As the maximum number of arguments was 3, the tail was 15 (t = 7 × (3 − 1) + 1). Owing to the good performance of addition as a linking function, this function was used in this study [1, 9, 16, 59]. In the next stage, the values of different genetic operators, such as mutation, crossover, were determined as presented in Table 3.

Table 3 GEP model parameters

2.5 Goodness of fit of model performance

To assess the different models employed in comparison with experimental data, the following statistical indices were used: three absolute error indices, i.e. Mean Error (ME), Mean Absolute Error (MAE) and Root Mean Squared Error (RMSE), the relative error index Mean Absolute Relative Error (MARE), and the statistical parameters coefficient of determination (R²), correlation coefficient (R), BIAS and ρ (Eqs. 7–14).

$${\text{ME}} = \frac{1}{n}\sum\limits_{i = 1}^{n} {(O_{i} } - P_{i} )$$

(7)

$${\text{MAE}} = \frac{1}{n}\sum\limits_{i = 1}^{n} {\left| {O_{i} - P_{i} } \right|}$$

(8)

$${\text{RMSE}} = \sqrt {\frac{1}{n}\sum\nolimits_{i = 1}^{n} {(O_{i} - P_{i} )^{2} } }$$

(9)

$${\text{MARE}} = \frac{1}{n}\sum\limits_{i = 1}^{n} {\left( {\frac{{\left| {O_{i} - P_{i} } \right|}}{{O_{i} }}} \right)}$$

(10)

$$R = \frac{{\sum\nolimits_{i = 1}^{n} {(O_{i} - \overline{{O_{i} }} ) \cdot (P_{i} - \overline{{P_{i} }} )} }}{{\sqrt {\sum\nolimits_{i = 1}^{n} {(O_{i} - \overline{{O_{i} }} )^{2} \sum\nolimits_{i = 1}^{n} {(P_{i} - \overline{{P_{i} }} )^{2} } } } }}$$

(11)

$${\text{Bias}} = \frac{{\sum\nolimits_{i = 1}^{N} {(P_{i} - O_{i} )} }}{n}$$

(12)

$${\text{SI}} = \frac{\text{RMSE}}{{\frac{1}{n}\sum\nolimits_{i = 1}^{n} {O_{i} } }}$$

(13)

$$\rho = \frac{\text{SI}}{1 + R}$$

(14)

where O_i is the observational value, P_i is the value predicted by the models, $\overline{{P_{i} }}$ and $\overline{{O_{i} }}$ are the means of the parameters and n is the number of parameters. R² (coefficient of determination), which is the linear regression line between the observed values and the values estimated by the models, was used to determine the model performance. RMSE, MARE and MAE values closer to zero indicate little difference between the values predicted by the models and the experimental values. The SI values (dimensionless form of RMSE values) were used for better comparison. The BIAS index represents how the models performed in estimating variables as negative and positive. Negative and positive BIAS values indicate model underestimation and overestimation, respectively. The models (GEP, 8 relations and NLR) should be compared with the experimental model using another suitable criterion and not only R. This is because R does not change meaningfully by shifting a model’s result values similarly, and the error functions only signify the error values and not the correlation in terms of RMSE and MARE. The ρ index was introduced by Gandomi and Roke [14].

3 Results and discussion

The first part of this section evaluates in detail the application of ten observational datasets to model learning. In the second part, the GEP and NLR models as well as available empirical relationships are verified, and stable channel shape is discussed. The third part addresses the bank profile shape suggested by the model introduced in this study. Finally, the model sensitivity to different input variables is analysed.

3.1 Data processing

In the present study, ten experimental datasets were utilized for model training to predict threshold channel bank profile [30, 40] (two sets), [6], Hassanzadeh et al. [29] (two sets) and four sets from the current laboratorial work). Each dataset is related to a specific laboratorial setup with different hydraulic conditions and sand particles applied for stable channel formation. In each laboratorial dataset, the Q (discharge) and D₅₀ (median grain size) values completely differ from each other. Hence, the models were trained in different discharge conditions, which is a significant advantage of the present study. The models were examined for different values of D₅₀ and discharge (Q) (hydraulic condition) as well as x (geometric parameter). Various profile shapes were obtained for each governing circumstance. Three variables, namely Q, D₅₀ and x (transverse distance from the channel centre), were used as input variables and y (vertical boundary level of points located on a stable bank profile) served as output data from the introduced model. In total, there were 276 laboratorial data for Q, D₅₀ and x and 276 data corresponding to y. From the total, four laboratorial datasets were utilized from the current research (155 data) for training, while four laboratorial dataset (51 data) from Ikeda [30], Mikhailova et al. [40] (two sets) and Diplas [6] were used for testing, and two datasets (71 data) from Hassanzadeh et al. [29] were used for model calibration. Therefore, different ranges of hydraulic conditions (Q in a high range of 2–69 l/s and D₅₀ in the range of 0.2–1.9 mm) and geometric variations (x in the 0–90.77 cm range and y in the 0–12.24 cm range) were utilized for model training so the extracted model results would be reliable.

3.2 Verification of existing methods in predicting bank profile characteristics

This section evaluates the performance of GEP, NLR and prior empirical relationships in predicting two threshold channel bank profile characteristics (x, y). The models were trained using ten experimental datasets with different hydraulic and geometric conditions. In the present study, in addition to artificial intelligence (AI), nonlinear regression (NLR) was also fitted to the experimental data to provide the following Eq. (15) for channel bank profile (y) prediction, where Q, D₅₀ and x are considered input data:

$$y = \;0.11628 \times Q^{ - 0.53536} \times D_{50}^{ - 0.08449} \times x^{1.53783}$$

(15)

Figure 5 presents scatter plots of y^* predicted by the GEP and NLR models in comparison with experimental values in training (current research experimental data), testing [30, 40] (two sets); [6]) and validation [29] (two sets). The figure shows the ± 10 and ± 20% error lines accordingly. Table 4 displays the error indices for the models with all ten datasets compared with experimental values.

Fig. 5

Comparison of y^* predicted by the GEP and NLR models with experimental results in a training, b testing and c validation

Table 4 Comparison of GEP and NLR models with experimental results according to various statistical indices

According to Fig. 5, the GEP model data compressed around the exact line and the data correlation percentage is high, with acceptable R² values approaching 0.9 in all stages. The R² coefficient in training was 0.975, which is very close to 1 and indicates high GEP model prediction accuracy. Moreover, almost 90% of data are within the ± 10% error lines and all data are located within the ± 20% error lines, signifying low model prediction error. The GEP models were validated with high-precision experimental datasets [29] and were in good compliance with the experimental results (R² = 0.9464). For the validation datasets, the fitted line almost coincides with the exact line. Moreover, few data exceed the + 20% error line. Hence, the GEP model results can be trusted in diverse practical cases. For the NLR model, data compression is not around the exact line and most data are located above the fitted (dotted) line. If the fitted line is at the right of the exact line, it means the model overestimated and if it is at the left, the model underestimated. With the NLR model, the fitted line is much to the left of the exact line (especially in testing), which represents model underestimation. In training, the GEP results were in acceptable compliance with the experimental results, with a high R value of 0.976. In the validation stage, the GEP model exhibited a high correlation value (R = 0.952), but a few data exceed the ± 20% error lines. Also with the NLR model, most data are in the positive error range and only a small percentage of data are scattered around the exact and − 10% error lines. According to Table 4 (for training and testing), the GEP model had R of 0.993 and 0.973 in training and validation, respectively, which are very close to 1 (the same values as for R²), indicating 100% model compliance with the experimental results. Moreover, the low relative and absolute error index values in all stages signify the high GEP model accuracy (MARE = 0.147 and RMSE = 0.064 with the validation dataset). Also according to the table regarding the validation dataset, the lower relative error index value (MARE = 0.147) compared to the corresponding testing (0.80) and training (0.188) values represents superior model performance in the validation stage. The higher validation values for other indices (RMSE = 0.064, ρ = 0.076) than training (RMSE = 0.034, ρ = 0.049) were due to model weakness in predicting high y values (close to the free water surface values), which produced high RMSE and MAE values.

With NLR, R was 0.976 and 0.952 in training and validation, respectively, which are very close to 1, signifying high model accuracy. However, compared with the GEP model (R = 0.938), this index value decreased by 16% in testing for the NLR model (R = 0.807). Moreover, the increasing ρ value for NLR in both modes (by about 3 times especially in testing), indicates the superior GEP model performance. The error index values of NLR were about 2.5 times greater than GEP (MARE = 0.375 and RMSE = 0.115). The negative and positive BIAS index values indicate model underestimation and overestimation, respectively. Table 4 shows that for the NLR model, this index in training and testing was − 0.0035 and − 0.068, respectively, which indicates model underestimation (Fig. 5). For the GEP model, the BIAS values very close to 0 indicate high model accuracy (BIAS = 0.0005 and − 0.013 in training and validation, respectively). The MAE index shows the absolute difference between the predictions and experimental results. This index value is almost 65% lower for the GEP model (the lowest MAE value of 0.026 in training) than for NLR (the lowest MAE value of 0.076 in training). That means the GEP model is more accurate than NLR and can predict stable channel bank profiles well. Besides, the high GEP model accuracy with different experimental data ranges and in all stages (especially in validation with the lowest relative error and high R coefficient) represents the applicability of GEP in most similar hydraulic and geometric circumstances. Figure 6 presents the genotype and phenotype [Expression Trees (ETs)] of a population individual related to the GEP model. In order to simplify these ETs, the pseudocode in Fig. 7 was used to predict bank profiles with different particle sizes and discharge rates.

Fig. 6

Expression trees for the GEP model

Fig. 7

Output program of the optimum GEP model

3.3 Comparison of GEP and NLR models with existing methods in stable bank profile shape prediction

In the present section, the results obtained with the GEP model are compared with those of 8 existing models. Table 5 shows the relative and absolute MARE and RMSE error indices for the different models [GEP, NLR and 8 theoretical equations (Table 1)] in comparison with experimental data from the present work and Ikeda [30] and Diplas’ [6] data for discharge rates of 1.157, 16.28 and 12.526 l/s. Figure 8 presents MARE index bar graphs for better comparison.

Table 5 Evaluation of GEP, NLR and 8 previous models in comparison with experimental data from the present study, and Diplas [6] and Ikeda’s [30] data according to the relative and absolute MARE and RMSE error indices

Fig. 8

MARE error index of bank profile characteristics predicted by different models in comparison with the corresponding experimental values from the present work and Ikeda [30] and Diplas’ [6] data

Figure 9 presents the threshold channel bank profiles modelled by GEP, NLR, GFM, CKM, BVM, IKM and GFM in comparison with the experimental values from the present work and Ikeda [30] and Diplas’ [6] data. Figure 8 and Table 5 demonstrates that the GEP model error was lower than previous models (MARE = 0.021 and RMSE = 0.0343) in training. After the GEP model, DEM and CKM exhibited the lowest error index (MARE of 0.12 and 0.1095, respectively). As seen in Fig. 9, these models performed almost the same and predicted a smaller cross section than the experimental outcome. The GFM model also calculated a small cross section and performed inefficiently, because the GFM equation does not consider lift force, which creates a sharp bank slope. Lift force is the main parameter affecting channel formation and equilibrium shape. The GFM model suggested a cosine curve as the channel shape, which is not a stable shape [7]. With three experimental datasets, CKM and GFM predicted smaller cross sections similar to other models but with a slight difference in error values. A channel with clean water and non-cohesive sediment particles was analysed. Based on the authors’ data, despite the drop in MARE error value (0.1095) due to the non-cohesive sediments in the experiments, the CKM model estimated a smaller cross section than the experimental cross section. Moreover, CKM suggested a parabolic curve according to Mironenko et al.’s [41] study, which is not a suitable shape. Concerning lift force and non-cohesive sediments, DEM estimated a small cross section. However, the results indicate that the DEM modelling process was similar to VDM and the current research data, and DEM underestimated the experimental data (MARE = 0.1200). Unlike Diplas and Ikeda’s data, the DEM model had quite a large error and was not as efficient as other models. After DEM, the PIM and VDM models had greater errors based on the present research data and calculated larger channel cross sections. The two models produced approximately the same error values (MARE = 0.3227 and 0.265 for PIM and VDM, respectively). Apart from Diplas and Ikeda’s data, the PIM and VDM models performed the best with low error values. As seen in Fig. 9 b, the highest compliance with experimental data was achieved by the VDM model. Therefore, PIM and VDM are introduced as the best among the other models. The VDM model yielded a three-degree polynomial for a stable bank profile and is introduced as the best and most accurate model for stable channel profile prediction [33]. With the PIM and VDM models, the momentum equations for fluid and the force balance equations for sediment particles in impending motion were solved by a numerical method. The momentum diffusion term was also considered in the numerical models. The VDM and PIM models suggested polynomial and exponential curve channel profiles. The VDM model is the modified case of Pizzuto’s equation [49, 56]. Ikeda’s data fit well on two exponential curves of DIM and IKM, so these models are introduced as highly accurate based on Ikeda’s data. Also according to Diplas’ data, IKM and DIM are among the best performing models after VDM and PIM. With the present research data, the IKM and BVM models had maximum MARE and RMSE errors and predicted much larger cross sections, which are not good results. IKM introduced a displacement coefficient and proposed a cosine curve, whose coefficient calculation involves complex bank profile equations and trial and error. BVM proposed two hyperbolic functions for channel shape, and it was found that the equations obtained from VDM made better estimations than other equations (based on the cosine curve), signifying that hyperbolic equations perform similar to the polynomial VDM [33]. In other research studies, it seems that models which include momentum diffusion (polynomial curve) predict a more logical threshold channel form, although the error values are higher than models which neglect this term (cosine curve) [49]. The NLR model underwent a similar process to the experimental model, but it significantly differed in value prediction from the three experimental datasets (especially the current study dataset).

Fig. 9

Bank profile shapes suggested by different models compared to the experimental model with a current study data, b Diplas’ [6] data and c Ikeda’s [30] data

Therefore, it can be concluded that the VDM model with MARE of 0.265 that suggested a logical polynomial curve was the superior model with data from the current study. With Diplas and Ikeda’s data, the VDM model (MARE = 0.04), and DIM and IKM (MARE = 0.06) produced the best performing relations.

With the data from the present study, the NLR model with MARE of 0.25 performed similar to VDM and proposed a similar shape as well. Compared to the other models, GEP with MARE of 0.034 was in high compliance with the experimental results and is introduced as the superior model with the data from the present study. Based on Diplas and Ikeda’s experimental data, the GEP model predicted the profile shape almost according to the experimental data and other models, but it predicted y values with a slight difference from the experimental data. This difference is on account of the varying hydraulic and geometric circumstances in each laboratorial work; therefore, the proposed GEP model can be considered an appropriate equation for any experimental and real-case condition. With both datasets, the GEP models functioned similar to DEM [5] with MARE of 0.2 and 0.3. With Diplas’ data, the RMSE for the DEM model (0.5) was greater than the GEP model (0.12). That is due to the weak performance of DEM with high y^* values, unlike the GEP model (Fig. 9b) with acceptable prediction values in this area. In Fig. 9 and according to all experimental data, CKM, and VDM and GEP proposed parabolic and polynomial curves for the channel, respectively. With the present study data, the BVM and IKM models proposed a cosine curve with a large difference from the experimental data, unlike Diplas’s and Ikeda’s data where IKM and BVM were the closest to the experimental values. GFM predicted a small and unsuitable stable channel cross-sectional shape with all experimental data. The next section investigates the curved shape proposed by the GEP model at different discharge rates and with different experimental data.

3.4 Bank profile shape predicted by GEP in different hydraulic conditions

Figure 10 compares the bank profile shape calculated by the GEP model based on different experimental data and discharge rates with the experimental values. Table 6 presents the error indices for the bank profile characteristic predictions made by the GEP models compared to different experimental values at various discharge rates. Figure 10 shows regression line plots for each GEP model and the fitted equation for each discharge rate.

Fig. 10

Stable channel bank profile predicted by GEP model and regression trend based on different laboratorial datasets at different discharge rates in comparison with experimental values

Table 6 Different error indices for bank profile characteristics predicted by the GEP model compared to experimental results at various discharge rates

The proposed shape of a threshold channel is therefore the “polynomial type” due to the transverse slope at the channel centreline, which is zero and equal to the position angle of sediment at the water surface. It is worth noting that unlike the models presented in the prior section, the channel shape is not a cosine curve, parabolic, exponential or a hyperbolic function. An evaluation of the diagrams for different discharge rates based on different experimental datasets indicates that with increasing discharge, the threshold channel’s cross section is wider and deeper. With Mikhailova et al.’s [40] datasets, a wider cross section is clear at high discharge of 69 l/s rather than at 65 l/s. Moreover, sudden cross section widening occurred near the free water surface with these datasets. In this condition, the side bank slope reduced. In natural channels, during greater flood periods, the water surface slope is lower. As the width and bank adjustment rates occur much lower than the depth adjustment, the discharge increases, causing river water surface deepening. With Hassanzadeh et al.’s [29] data, the GEP model predicted the side bank slope reduction well with increasing discharge up to 17.96 l/s, but the difference between predicted values and the corresponding experimental data was slightly greater than the values predicted at 12.07 l/s. According to the error values in Table 6, with all experimental datasets and at different discharge rates, the error values decreased with increasing discharge and model efficiency increased except for Hassanzadeh et al.’s [29] dataset. With this dataset, the error values for two discharge rates were nearly equal, with slightly higher values at high discharge of 17.96 l/s. As mentioned previously, near the free water surface, the efficiency reduced slightly compared with the experimental values. With Mikhailova et al.’s [40] datasets, the RMSE value at 65 l/s (0.094) was less than at 69 l/s (0.122), unlike the MARE and R values. It can be said that the GEP model was weak in predicting the y value near the free water surface and could not predict the sudden channel widening. Therefore, the RMSE value, which is the squared difference between the model and observational values increased at this water surface level. Based on Ikeda’s [30] data, the GEP model with higher MARE (0.8) than the experimental datasets exhibited low efficiency in predicting y. With Ikeda [30] and Diplas’ [6] datasets, despite the high difference between the model and experimental values, GEP predicted the bank profile shape trend similar to the observational values.

With the present study data, the statistical index values were better at the 1.157, 2.57 and 6.2 l/s discharge rates, because the experimental channel section in all three modes was the same (trapezoidal) and at 2.18 l/s the channel section was compound. It can also be concluded from Table 6 that with increasing discharge, the relative and absolute error indices decreased and the R coefficient value increased. Therefore, it can be said that with increasing discharge GEP model accuracy increased and it performed the best at 6.2 l/s with the lowest index errors (R = 0.994, MARE = 0.143, RMSE = 0.042). At this discharge rate, the absolute difference between the predicted and experimental data (MAE = 0.030) was very low (about 3%).

The proposed GEP model exhibited acceptable performance in all stages of training, testing and especially validation. Moreover, the GEP model was the most efficient with Hassanzadeh et al.’s [29] validation dataset compared to other datasets. Hence, the proposed GEP model is applicable in different flow hydraulic and geometric circumstances. The GEP model could predict the bank profile trend the same as the laboratory measurement despite the small differences in some cases. It can be seen that the best fitted line is a polynomial curve, which is in complete compliance with the GEP model for all datasets.

3.5 Sensitivity analysis

In the present study, the effect of the Q, D₅₀ and x parameters on estimating y (boundary elevation of a stable channel bank profile) was evaluated using sensitivity analysis. To analyse the y variable change trend according to the Q, D₅₀ and x input variables, partial derivative sensitivity analysis was applied to the equation extracted from the GEP model. With this method, the partial differences between the output variable and each input parameter were used to investigate the sensitivity results of input parameter x_i. It is clear that much higher partial derivatives indicated greater input variable effect on the results. If the derivative value was positive, an increase in input parameters led to an increase in the output variable. The sensitivity analysis of the GEP model is shown in Fig. 11 for bank profile characteristic prediction based on Mikhailova et al. [40], Ikeda [30], Diplas [6], Hassanzadeh et al. [29] and the current study authors’ experimental data.

Fig. 11

Sensitivity analysis results for different input parameters: aD₅₀, bQ and cx in bank profile characteristic prediction by GEP with different experimental datasets

Figure 11 indicates that at D₅₀ < 0.6 the sensitivity values are positive, signifying the strong effect of this parameter on y value prediction. With increasing D₅₀ (D₅₀ > 0.6), the sensitivity values gradually tend towards negative, meaning that the parameter’s effect on y prediction reduced in this range. In evaluating the effect of Q, it can be said that at low discharge (almost Q < 8 l/s), the sensitivity values are negative and positive (at very low discharge) and with increasing discharge (Q > 8 l/s) the effect of this parameter rises. In evaluating the effect of parameter x on y value prediction, the sensitivity values in all x ranges are positive, affirming the strong effect of x on y prediction. At x < 20 the sensitivity values increase to high values on the axis (~ 1), demonstrating the strong effect of this parameter in low x value ranges. With increasing x (x > 40), the effect of this parameters on y value prediction is fixed.

4 Conclusions

In this study, we examined GEP model performance in estimating a vertical boundary level located in the bank profile of a threshold channel. The GEP model was trained, tested and validated based on ten sets of laboratorial data (276 data in total) with different hydraulic and geometric conditions. A vast experimental study was done in order to measure the stable bank profile shape in different hydraulic conditions. A robust and practical relationship was achieved from the proposed GEP model, while a nonlinear regression model was fitted on the same observational data. In addition, different relationships extracted by previous researchers based on regression, numerical and analytical methods were tested for comparison with the presented GEP model in order to assess the models’ efficiency in terms of various observational data. Furthermore, sensitivity analysis was done to evaluate the impact of different parameters such Q, d₅₀ and x related to each point on GEP model performance. The results demonstrate that GEP model performance was acceptable with low error indices in all stages and especially in the validation stage. Therefore, the GEP results can be trusted in a range of hydraulic and geometric channel conditions. Based on the authors’ current experimental data for GEP model training, the GEP model introduced performed the greatest compared with different prior models, with lower error indices. Based on all available experimental datasets, the GEP model generally predicted the bank profile shape trend (by suggesting a polynomial equation) similar to the experimental data despite the small error between predicted and experimental values. The GEP model suggested the polynomial shape for the cross section of a stable channel, which was also expressed by the VDM and PIM models. A great advantage of the proposed GEP model is that it presents a reliable equation suitable for different hydraulic and geometric conditions. The equation is capable of predicting the vertical boundary elevation of a bank profile and can be utilized as an alternative to previous traditional methods of practical predesigning. However, the presence of various functions and operators in the relationship proposed by the GEP model leads to higher GEP model complexity compared to previous analytical and regression-based methods. Therefore, we suggest using other computational intelligence method functions based on evolutionary algorithms to estimate the bank profile shape of stable threshold channels and compare the results with those from the present study.